我们把一则故事中，可以简化成[-R，+R]的一组母题称为对称母题。R表示母题中事件的内容，“-”与“+”表示该事件或行为对于我们的分析对象是否有利。例如故事中主人公“遭遇难题”与“解决难题”，这两个母题对应的事件内容是“难题”，即R=难题；遭遇是使主人公陷入不利的境地，即“-”，解决是对不利状态的消除，即“+”。如此，这一对母题可以表示为[-难题，+难题]。又如[-救助，+救助]、[-恩惠，+恩惠]，等等。这一对母题类似于数学中的相反数，而相反数以原点为轴心具有对称性，我们可以类比，将这一对母题看作是具有对称性的母题，如图1所示。

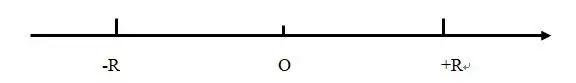
图1 对称母题图示

需要特别强调的是，母题层面的对称结构只能针对同一角色的行为或状态来界定。例如在《狗耕田》中，兄弟分家，弟弟只得到一片荒地和一条狗，缺少耕田助手，狗主动帮助弟弟耕田，并且耕得又快又好，哥哥得知后把狗借走，但是狗来到哥哥这里就不再耕田。在这一段故事中，我们需要厘清“缺少助手”“狗耕田”“狗不耕田”这三个母题的关系。构成对称结构的是“缺少助手”与“狗耕田”这两个母题，它们可以被简化为[-助手，+助手](如图2)。而“狗耕田”与“狗不耕田”这两个母题，虽然都是由狗完成的，但狗并不是我们的分析对象，狗的不同行为针对着弟弟（主人公）和哥哥（反角）这两个不同的分析对象，因此不能被视做对称母题。

图2 《狗耕田》中的对称母题

对称母题的实质是在故事中先后出现了两次转折，第一次转折是让人物偏离原本的轨迹，第二次转折是对第一次转折的消弭，使人物回到原本的状态。根据转折发生的原因，可以将对称母题分为如下两个大类：

（一）人物自主行动产生的对称母题

这一类对称母题是由主人公的自主行为引起的。最典型的就是在报恩型故事开端，主人公先捕获一只动物或是援救一只受伤的动物，在动物的伤病好了之后把它放走，或直接放生。例如在《渔夫和龙女》中，渔夫费了九牛二虎之力捕获了一条金鱼，但是在金鱼的恳求下，渔夫把它放回了水中。“捕鱼”和“放生”这一对母题可以简化为[+鱼，-鱼]。我们也可以用坐标轴来表示故事中渔夫的经历。如图3，线段+a表示渔夫捕获一条金鱼，线段-a表示渔夫把这条鱼放回海里，经历两次转折之后，渔夫又回到最初一无所有的状态，这两个母题呈现出对称关系。

图3 《渔夫和龙女》人物经历图

（二）外在因素产生的对称母题

在大多数故事中，情节转折是由外在因素造成的，即故事本身为主人公设置了不利因素，或是故事中的其他角色给主人公设置了“障碍”，使主人公的生活轨迹发生了变化。在后续发展中，障碍被解除，主人公又回归到正常的生活轨迹。这类对称母题又可以分为两类。

1.非人为因素产生的对称母题

在很多故事中，缺乏或困境等负面状态是故事起始时的设定，也是情节发展的动力。例如《哥仨找药》的故事，开头就说国王患了眼疾，遍访名医也没能治好，云游和尚说只有让国王亲近的人去找来光明露，才能治好国王的病。故事开头就将国王置于缺乏药物的状态。后来三个王子都外出找药，小儿子通过考验，带回光明露，治好了国王的眼疾。在这个故事中，国王经历了[-药物,+药物]这一组对称母题。图4是用坐标轴表示的该组对称母题，-a是故事初始时的缺乏状态，+a是结尾处缺乏的消失。

从这个例子中我们也可以看出对称母题虽然必须符合时间逻辑，但并不一定前后相继，可以在故事的首尾形成呼应。

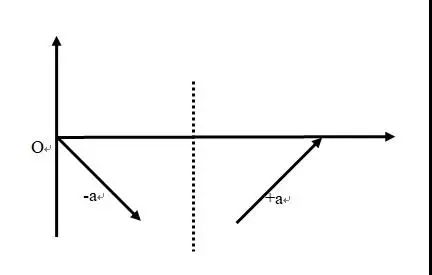
图4 《哥仨找药》人物经历图

2.人为因素产生的对称母题

人为因素产生的对称母题是故事中的其他角色给主人公设置了障碍，使故事情节发生转折，在这种情况下，同一情节会出现两组对称母题。例如《十兄弟》的这一段情节：

县官不问青红皂白，就叫抓人问斩。这事被听声一听到了，忙说给兄弟们听。硬颈二说:“你们去躲起，要斩叫他斩我。”公差把硬颈二抓到衙门，县官喝令开刀斩首。刽子手刀砍斧劈，斩了半日硬颈二身上记号都冇得一点。县官吓得忙把他放了。

这段情节中，十兄弟作为主人公，是同一个角色的十个分身，所以无论县官要缉拿谁，在这里都是同一个角色遭遇困境，对于县令而言则是设置困境。在后续发展中，主人公凭借自身特性让县令未能得逞，解除了困境，对于县令而言则是他设置的困境被解除。从简化形式看，两者对应的对称母题都是[+困境，-困境]，但是不同角色在坐标轴上对应的矢量方向是不同的。如图5，实线是主人公的经历，-a表示他遇到了困境，即对他不利的行为，+a表示他凭借自身本领解决了困境；双实线是县官的经历，+a’表示他给主人公设置了难题，对他而言是有利的行为，-a’表示困境被主人公破解，没有产生实际效果，对县令而言是不利的。

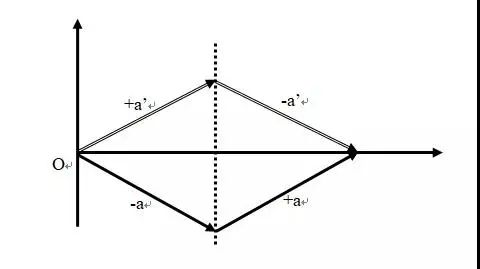
图5 《十兄弟》人物经历图

情节就是故事中的母题链，对称母题连接在一起就是一段情节，所以对称母题是对称情节的基础。反过来说，对称情节就是由对称母题叠加或重复所得。母题层面的对称结构仅针对单一人物的行动或状态来界定，但是一则故事中，承担对称母题的角色不只一个，因此除了单一人物对应的对称母题叠加形成对称情节外，不同角色对应的对称母题之间也可以叠加，构成多层次的对称情节。

通过上文分析，我们可以发现无论哪种类型的对称母题，其本质都是情节转折。因此在划分对称情节的类型时，只考虑形式特征。

（一）串联式对称

当单一人物对应的多个对称母题的前半部分和后半部分，分别累加成固定情节，并依次出现在故事中时，坐标轴上用于标示这段情节的矢量线段，会形成类似于用电器首尾依次相连的串联电路图的图示，我们将这种对称情节称为串联式对称。以一个含有娶妻情节的求好运型故事为例：

 孤儿王小二是地主柳九舟家的长工，他和柳九舟的女儿如烟情投意合，并且想娶如烟为妻。图6中的OT表示王小二想要迎娶地主女儿。

地主柳九舟得知后，让王小二找来三斗三升瓜子金、二十四颗夜明珠和一张白狐狸皮。线段-a、-b、-c分别表示主人公面临的三个难题，这三个连续的不利因素在主人公和他的心愿之间构筑了一道障碍，使他又回到了起始状态。

 于是王小二向土地求助，土地指引他去西天问佛，并且委托王小二帮自己询问什么时候能升官。在去西天的路上，王小二又分别遇到白狐狸和乌龟，狐狸委托他询问佛祖自己什么时候能修成正果，乌龟委托他询问佛祖什么时候可以蜕壳成人。王小二见到佛祖，把土地、狐狸、乌龟的疑问告诉了佛祖，佛祖让王小二转告它们每个人应该舍弃的东西，此时王小二已经没有机会再问自己的事了。这一段故事与王小二的难题没有关系，因此在坐标轴上被省略。

在回家的路上，王小二向乌龟、狐狸和土地转述了它们各自问题的答案，它们把自己的东西送给了王小二，王小二恰好得到了地主让他找来的东西。坐标轴中的+c、+b、+a分别表示王小二得到狐狸皮、夜明珠和瓜子金，解决了难题，最终达成了自己的心愿。

 从母题层面来看，[-a，+a]、[-b，+b]、[-c，+c]是主人公对应的三组对称母题。在地主的要求下，主人公连续出现缺乏状态，-a、-b、-c可以连接成一段情节，同理消除缺乏的+c、+b、+a也是一段连续的情节，由于母题之间具有对称性， [-a，-b，-c]与[+c，+b，+a]在情节层面形成对称结构。

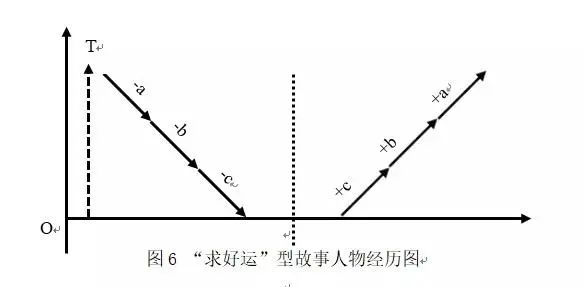
图6 “求好运”型故事人物经历图

（二）并联式对称

 在一些故事中，不同角色会对应相同的对称母题，当这些对称母题前半部分和后半部分分别累加成固定情节时，在坐标轴上就会形成类似首尾分别相连的并联电路图的图示，我们称这类对称情节为并联式对称。云中落绣鞋型的故事中通常会出现这样的情节，例如在《救皇姑》中，当主人公被反角陷害，滞留洞中后出现了这样一段情节：

再说常兴见皇姑吊上去后，等了很久不见筐子下来，没办法，又往里走，边走边瞧，看见在一个石柱上，用铁绳绑着一条蛟龙，流着眼泪在哭。常兴对蛟龙说:“你怎么绑在这里了？我能救你吗？”蛟龙听了说:“你把我头上的泰山取掉，不要取绑我的铁绳。”常兴就把蛟龙头上的一张咒语取掉了，蛟龙一动，铁绳就脱落下来。这时，蛟龙说:“恩人，你骑到我的背上，把眼睛闭了，千万不要睁开，也不要出声。常兴听了就骑到蛟龙的背上，眼睛一闭，只听得耳旁有风声响。不一会儿，蛟龙说:“恩人，你把眼睛睁开吧！”

我们同样可以把主人公和蛟龙的经历与行动在坐标轴中表示出来。-a、-b分别表示主人公落难和蛟龙落难，+b、+a表示蛟龙和主人公分别获得解救。从母题层面来看，[-a，+a]和[-b，+b]是主人公和蛟龙分别对应的一组相同的对称母题，即[-救助，+救助]。从情节层面来看，主人公和蛟龙先后在同一个地方落难，又先后获救，因此[-a，-b]与[+b，+a]是两段连续的情节，同样由于母题间的对称性致使这两段情节成为对称情节。

在并联式对称中，每个角色的行动与状态都是独立的，虽然有时间上的先后关系，但是一个角色的状态并不会累加在另一个角色的状态之上，这也是串联式对称与并联式对称的区别所在。

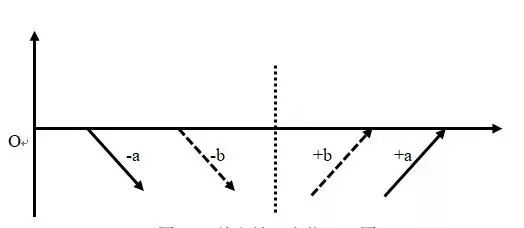
图7 《救皇姑》人物经历图

（三）多重式对称

当单一角色或不同角色对应的相同的对称母题以完整形式重复出现时，故事情节会形成多重式对称。例如在《娶皇姑》中：

主人公是一个以讨饭为生，但是心地善良的穷小伙。他在讨饭途中救了一只快被淹死的蚍蜉、一只生病的老鼠以及一只落水的飞蛾。图8坐标轴中的线段-a、+a、-b、+b、-c、+c表示动物们落难并且获救的情节。

 后来，主人公遇到了一个白胡子老人，老人告诉他，皇帝正在张榜招婿，他有娶皇姑的命，并指示他去京城揭皇榜。主人公到了京城，揭下皇榜，见到皇帝。皇帝决定对他进行考验，首先把他关到一个屋子里，让他用一晚上时间分开沙子和米。主人公进屋后，想起自己一天没吃饭，饥肠辘辘，这个时候老鼠给他叼来了馒头。他吃饱之后又对着沙子十分发愁，边捡边哭。这时，被他救过的蚍蜉带着一群蚍蜉前来相助，帮他分开了米和沙子。第二天皇帝又让他在十二顶花轿里选出皇姑所在的轿子，在飞蛾的帮助下，他成功地选出了皇姑的轿子。这一段情节对应着图8中的-a’、+a’、-b’、+b’、-c’、+c’。

这前后相继的两段情节，由[-困境，+困境]这组对称母题重复六次构成，也就是坐标中的[-a，+a]、[-b，+b]、[-c，+c]、[-a’，+a’]、[-b’，+b’]、[-c’，+c’]。在由[-a，+a]与[-a’，+a’]构成的情节中，落入困境的角色和实施救援的角色之间发生了置换，因此这两段情节之间形成了对称关系。同理[-b，+b]与[-b’，+b’]、[-c，+c]与 [-c’，+c’]也是具有对称性的情节。在这个故事里，-a、+a、-b、+b、-c、+c 连续出现，即动物连续落难并被主人公援救，而-a’、+a’，-b’、+b’，-c’、+c’则是主人公连续遭遇困境，在动物的帮助下困境被顺利解除。由于组成这两段长情节的次级情节之间具有对称性，那么 [-a、+a，-b、+b，-c，+c]与[-a’、+a’，-b’、+b’，-c’、+c’]在故事层面构成了第三重对称。

图8 《娶皇姑》人物经历图

（四）混合式对称

在一则完整的幻想故事中，上述三种类型的对称情节可以独立存在，也可以组合出现，构成混合式对称情节。例如，前文提到的带有娶妻情节的求好运型故事，我们在分析故事中的串联式对称情节时只讨论了主人公王小二的经历。然而故事中的土地、狐狸和乌龟分别对应了[-升官，+升官]、[-成仙，+成仙]、[-成人，+成人]的对称母题，这三组对称母题可以叠加形成并联式对称情节。如图9中的[-d，-e，-f]与[+f，+e，+d]。由此可见，该故事由串联式对称情节与并联式对称情节混合而成。

 从更为宏观的故事层面来看，这两种对称情节的前半部分和后半部分拼接成的情节，即[-a，-b，-c，-d，-e，-f]与[+f，+e，+d，+c，+b，+a]也具有对称性。体现在故事情节上，即在故事前半部分，无论是主人公王小二，还是土地、狐狸和乌龟，都处于缺乏彩礼、未能升官、成仙以及蜕壳成人的不利状态，我们可以将描述他们不利状态的情节合并为-R。故事的后半部分，所有角色的不利状态被依次破解的情节可以用+R表示，合并相同状态的情节之后，整个故事呈现出[-R，+R]的对称结构。

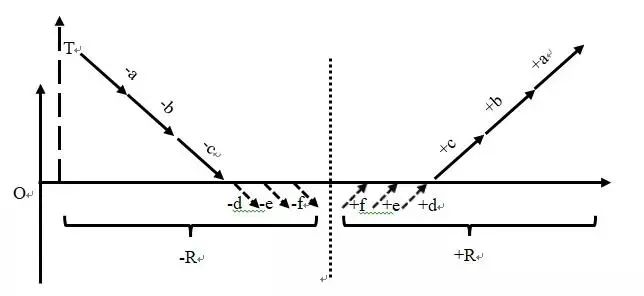
图9 “求好运”型故事人物经历图

母题与情节的对称法则是故事发展过程中的规律，而母题和情节都与故事中的人物息息相关，人物是转折情节的发起者，或是承受者。因此在幻想故事中，对称情节往往会导致故事中的人物配置出现对称结构。

配置是指故事赋予人物的有关属性、身份、财富等方面的设置。一则故事会在人物第一次出现，或是发展到一定阶段的时候赋予人物一定的配置。对称配置是指故事结尾处仍然保留初始时的配置，没有增减，但会发生转移或置换。我们可以根据维持配置对称的人物数量将其分为两大类。

（一） 单一人物的对称配置

单一人物的对称配置是指故事中，单个人物前后状态、属性或者身份没有发生变化。根据人物的初始状态可以分为“负向对称”和“正向对称”两类。

1.负向对称

幻想故事中，最初处于不利状态的主人公并非都能改变自己命运，有些主人公在折腾了一圈之后，又回到了最初的状态。我们把这种情况称为负向对称。最典型的就是《渔夫和金鱼》的故事。最初，渔夫和妻子在海边的破屋中过着清贫的日子，我们用N点表示渔夫起始状态。有一天，渔夫捕获了一条金鱼，然而在金鱼的恳求下，渔夫把它放走了，失去了金鱼，图10中的[+a，-a]表示的就是这一组对称母题。接着渔夫获得了金鱼赠予他的财富，然而因为有人违反了不能贪得无厌的禁忌，渔夫失去了所有财富，[+b，-b]表示得到馈赠和失去馈赠的情节。故事结尾处，渔夫又回到了开始时一无所有的状态，即N’点。从图中我们可以看出，在经历了两次转折之后，渔夫的状态没有发生变化，仍旧处于一贫如洗的的负向状态。

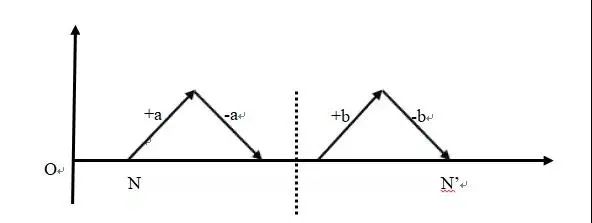
图10 《渔夫和金鱼》人物经历图

2.正向对称

另一些故事中，最初处于负向状态的主人公在经历了一系列事件之后，命运发生了逆转，变为正向状态。此时故事中的反角，出于不同目的，向主人公的正向状态发起挑战，通过设置考验或难题等方式，企图剥夺主人公的正向状态。主人公总能成功解决所有的难题和考验，在故事结尾处，仍旧保持正向状态。

例如在龙女型故事《张砍柴和李打鱼》中，为了感谢张砍柴的救命之恩，龙女以身相许，成为了张砍柴的妻子。此时主人公处于正向状态，即图11中的P点，这也是对称配置的起点。当县官得知张砍柴娶了一位有魔法的娇妻之后，心生嫉妒，想把张砍柴的妻子占为己有，于是给张砍柴出了一道三天砍三百担干柴的难题，告诉他如果完不成就要交出妻子；龙女得知后，利用法术变纸为人，帮张砍柴解决了难题，这段情节为图11中的[-a，+a]。县官不肯罢休，又让张砍柴去找“没意思”，在龙女的帮助下，张砍柴从龙宫得到一个盒子，交给县官，告诉他这就是没意思，县官打开盒子，里面冒出来了一个火球，烧光了县衙。这段情节是坐标轴中的[-b，+b]。最终张砍柴和龙女又过上了安稳幸福的日子，即图11中与P点对称的P’点。与负向对称一样，主人公在经历了两次转折之后，同样也回到了起始状态，不同的是，主人公始终处于有利的境地。

图11 《张砍柴和李打鱼》人物经历图

（二） 对立人物的对称配置

如果我们把同一则故事中，主人公和反角的状态与经历标示在同一坐标轴上，可以发现，在同一时刻，主人公和反角配置的叠加也呈现对称结构。根据两者前后状态是否一致，可以分为平移型对称和倒置型对称。

1.平移型对称

平移型对称是指故事中主人公和反角的配置前后没有发生变化。我们把《张砍柴和李打鱼》这个故事中县官的行为和状态用双实线标示在坐标轴上，可以得到图12。主人公的经历与上图一致。对于县官而言，他的愿望是夺取龙女，与拥有龙女做妻子的主人公相比，他处于负向状态，在坐标轴中，县官的起始点为N点。后来他给主人公出了两道难题，被主人公一一解决（图12中[+a’，-a’]、[+b’，-b’]）。最终他仍然没有得到龙女，还是处于负向状态（N’）。

这段情节首尾两端人物的配置都是正向状态和负向状态的叠加，前后对称。并且两个人物的配置保持一致，主人公始终是正向状态的，反角也一直处于负向状态，因此是平移型对称。

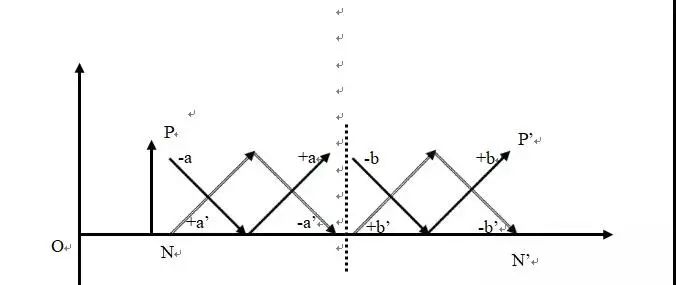
图12 《张砍柴和李打鱼》人物经历图

2.倒置型对称

另外一些故事中，虽然主人公和反角在首尾两端的配置均为正向状态和负向状态的叠加，但是却发生了置换，故事开始时，处于负向状态的人物在结尾转为正向，处于正向状态的人物转为负向。

在我们熟悉的《狗耕田》里，兄弟两人的在故事首尾的状态就就是倒置型对称。如图13，我们以分家之后，兄弟两人一贫一富作为起点，弟弟（主角）和哥哥（反角）的经历分别从N点和P点开始。对于弟弟而言，+a表示狗帮他解除了缺乏助手的困境，+b则是弟弟得到了额外奖励。-a则是狗不配合哥哥，并且被哥哥杀害，-b是哥哥被惩罚。在故事的首尾两端，虽然兄弟两人的配置发生了倒置，弟弟从负向状态（N）转变为正向状态（P’），而哥哥恰好相反，但是同一时刻都是正向状态和负向状态叠加，因此具有对称性。

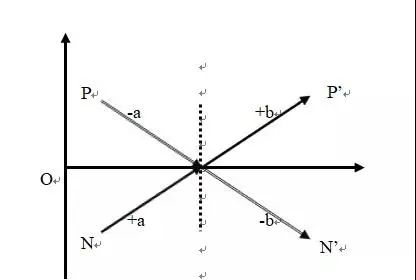
图13 《狗耕田》人物经历图

通常情况下，当人物起始的负向状态得到改善，但是他本人或者其他相关人物违反了故事中的某些规则时，他又回归到负向状态，这时就会出现负向对称。而正向对称，通常只出现在主人公身上，引起他状态变化的原因必定是反角设置了障碍。最终主人公一定能够克服所有的障碍，回到最初的正向状态。给主人公设置障碍的反角则经历了负向对称，这两者状态叠加就形成了平移型对称。倒置型对称通常出现在主角处于负向状态并且反角处于正向状态的情况下，主人公和反角经过几轮较量，配置发生逆转。主人公获得财富、名望或是美满的家庭等，而反角则失去曾经拥有的一切。

在对幻想故事中的对称法则有了一定的认识之后，我们可以进一步探究幻想故事中的对称法则有什么意义。

从审美角度来看，对称作为一种叙事法则，源自人们对于对称的特殊偏好。审美心理学研究表明，对称性是影响审美偏好评价的重要因素，对称性与“美”的审美判断之间相关度极高。格式塔心理学家认为一个好的图形是完整的，倾向于对称、平衡和成比例的，对于一个不完整的图形，人们会在知觉的过程中将其补足为完整的。故事中的对称结构具备完整感与规律感，母题、情节以及人物配置在时序上前后呼应，符合人们的审美心理需要。    

从叙事功能的角度来看，对称结构是幻想故事某些“通则”在结构上的体现。对于对称母题而言，在一则故事中，主人公面临的障碍，无论是“难题”、“困境”还是“缺乏”，一定会被恰到好处的解除。不能多也不能少，倘若障碍没有完全解除，主人公仍旧陷于困境之中，没有回到正常生活轨迹，下一个转折就无法出现，故事也就进行不下去了；倘若解除的障碍超越了障碍本身的范围，例如助手在解除困境的时候还附赠了主人公一堆东西，或者直接将反角处死，一步到位的解决了问题根源，故事也就失去发展空间。

对称情节是幻想故事中的“巧合”在结构上的体现。如果主人公救助了三个动物，那么他之后一定会得到三次帮助；如果考验主人公的人向主人公索要三件物品，那么主人公一定能遇到可以提供给他这三样东西的人或动物，当主人公通过舍己为人的方式帮助了这三个人或动物之后，便能换得自己需要的东西。这也说明故事是一个封闭系统，不会出现无意义的人物。对称情节总能带给读者或听众意料之外、情理之中的惊喜感。

人物配置对称则说明幻想故事有一套绝对的是非善恶观念。在故事结尾处我们永远不会看到在好人得到好报的同时，坏人因为真心悔过也得到了好报；也不会看到当坏人被惩戒之后，好人并未得到应有的奖赏。这样的结局不符合故事的对称法则。

综上所述，经由对称母题的叠加组合，形成了对称情节，对称母题和对称情节都是服务于故事人物配置的对称性。母题、情节与配置以各种方式组装在一起，构建了接连不断的转折，增加了故事的趣味性，又使情节合情合理，故事的价值观也在这个过程中得以彰显。

 对称法则是以大量故事为样本，通过归纳得出的结论，我们可以将对称法则及其叙事意义代入一个前文未曾提及的故事中，在已知前半段情节的情况下，利用对称法则推演后半段情节，再与原版故事进行对比，进而对对称法则予以验证。

以《青蛙的麻胆》这个故事为例：

前文梗概：主人公在上学的路上遇到了一只青蛙，他每天都从自己的干粮里分出一部分来喂青蛙。主人公的爷爷发现主人公日渐消瘦，就跟踪主人公，想看看究竟发生了什么，结果爷爷被青蛙吓死。主人公责问青蛙，青蛙说它一定会报答主人公的，前提是主人公要先帮助它修炼。主人公为青蛙找了一块空地，青蛙修炼成仙之后，把自己肚中的麻胆赠予主人公，并告诉主人公用麻胆在死东西身上一摸，它就能复活，但是千万不能救人。主人公用麻胆救活了一条蛇、一只蚂蚁和一只蜜蜂。后来他遇到了一个死人，出于好心，他违反了禁忌，把这个人救活了（在后文中，这个人不断给主人公设置障碍，是与主人公对立的角色，下文用“反角”指称这个人）。反角问主人公用什么把他救活的，主人公说是青蛙麻胆，反角建议主人公把麻胆献给皇帝，换取官职，于是两人一同进京献宝。路上，反角心生歹意，把主人公推入井中。自己带着宝物去了京城，成为进宝状元，还娶了员外的女儿。而主人公在井里遇到了一条青龙，青龙帮助他从井里逃了出来。

在前半段故事中，出现了[+麻胆,-麻胆]、[+禁忌,-禁忌]以及[-困境,+困境]这三组对称母题。在情节层面，出现了主人公救助三个动物的桥段。在人物配置上，反角偷走麻胆献给皇帝，得到了进宝状元的头衔，并且迎娶了员外的女儿，处于正向状态，而被他陷害的主人公则处于负向状态。

根据对称法则，后文中主人公一定会遇到三次困境或难题，而被主人公救助的三个动物会帮助主人公解决这三个难题；在人物配置上，目前主人公和反角分别处于负向状态和正向状态，根据倒置型对称，故事结尾处主人公和反角的配置一定会发生逆转，主人公会夺回进宝状元的头衔和员外女婿的身份，而反角则会回到一无所有的状态。

后文梗概：主人公到京城之后找到了反角，但是反角却将他驱逐出门。正巧这时主人公遇见了被他救活的蛇，并向蛇诉说了自己的经历。蛇想出了一条计谋，它把员外的女儿咬伤了，员外贴出告示，谁要是能治好他女儿，就把女儿许配给谁。主人公按照蛇的指示治好了员外女儿，但是员外后悔了，于是出题考验主人公，让他在三天之内分开菜籽和胡麻的混合物。正在主人公焦头烂额之际，被主人公救活的蚂蚁带领蚁群帮助主人公顺利完成任务。员外还是不愿意履行承诺，他让主人公在十二顶轿子中选出自己的女儿。在蜜蜂的帮助下，主人公又破解了难题。员外十分好奇为什么主人公能解决所有的难题，主人公就把自己的经历和反角的恶行告诉了员外，员外又转告皇帝，皇帝命人查明真相后，夺取了反角的头衔，加封主人公为献宝状元，主人公也迎娶到了员外女儿。

根据对称法则，我们准确预测到了主人公会遭遇三次困境或难题，在被他救助过的动物的帮助下，他脱离了困境并且解决了难题。同时我们对主人公和反角的结局预测也是准确的。主人公成了献宝状元和员外女婿，而反角则被夺去了所有的荣耀和财富。

但是故事后续部分也出现了很多我们始料未及的细节。首先“员外”就是一个出乎意料、但是对故事情节发展至关重要的角色，员外是给主人公直接设置难题的角色，也是主人公和反角的状态与配置发生扭转的中介。其次从情节上看，我们没预料到当主人公被反角驱逐，陷入走投无路的困境时，蛇通过咬伤员外的女儿，让主人公和员外取得联系，并成为员外女婿的候选人；我们也没有预测到主人公遭遇难题的具体原因是员外后悔将女儿许配给主人公，想通过这样的方式考验主人公；也没有预料到两道难题分别是让主人公区分开菜籽和胡麻合的混合物以及从十二顶轿子中找出员外女儿。

由此可见，对称法则只是幻想故事的结构规律，当我们得知一个故事的前半段时，可以根据对称法则对故事后半段的发展方向做出大致预测，至于具体的细节和内容，则是对称法则力所不及之处。

当我们将幻想故事中的转折情节、人物的始末状态标示在坐标轴上后，得出了幻想故事的对称法则。对称法则设定了故事情节的大致走向与人物的命运状态，但这只是我们将故事情节抽象化之后得出的结构性规律。至于这些走向如何完成？由谁完成？人物的始末命运之间发生了什么？只要合乎情理，可以任意编排，并填充到对称法则搭建的框架之中。对称结构和具体情节的关系恰好体现了民间故事稳定性和变异性之间的张力。

综上所述，在幻想故事中，单一人物先后经历的两次内容一致、作用结果相反的事件构成母题层面的对称结构，根据事件发生的原因，可以将对称母题分为“人物自主行动产生的对称母题”与“外在因素产生的对称母题”。对称母题以不同方式叠加组合，构成“串联式”“并联式”“多重式”以及“混合式”的对称情节，揭示了故事中“巧合”的结构机制，使故事层次更为丰富多样。母题和情节的对称又促成故事中单一人物或对立人物之间的前后配置，以平移或是倒置的方式维持不变，形成人物配置对称，昭示了潜藏在民间故事中的伦理观。对称法则不仅具有审美效用，也是民间故事的叙事“通则”在形态学上的呈现，同时揭示了民间故事稳定性的结构奥义。

之前学者对民间故事中的“重复”与“对比”有过详细的论述，但故事中的对称法则却少有人提及。事实上，普罗普在对神奇故事的功能项研究中已经发现“有很大数量的功能项是成对排列的（禁止——破禁、刺探——获悉、交锋——战胜、追捕——获救）”。普罗普所说的“成对排列的功能项”与本文提出的“对称母题”在内涵上基本一致，都是单一人物经历的两次具有相同内容的转折性事件。对称母题的提出，以及对在对称母题基础之上形成的故事情节和人物配置层面的对称结构进行讨论，是向民间故事叙事本位研究回归的尝试，从本体研究视角，揭示了幻想故事的叙事规律与叙事动力机制，对民间故事“如何存在”的问题给出一个新的解题思路。